Como calcular a distância sabendo o ângulo

Comstock/Stockbyte/Getty Images
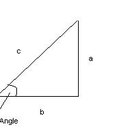
O ângulo de elevação é o ângulo entre uma linha imaginária horizontal e a linha de visão de uma pessoa focando em um objeto acima dessa horizontal. Uma reta pode ser desenhada do objeto para a horizontal, criando um ângulo de 90 graus. A pessoa, o objeto e a intersecção das retas criam os três pontos de um triângulo retângulo. Usando o ângulo de elevação e a altura do objeto a partir da horizontal, é possível encontrar a distância entre a pessoa e o objeto.
Step 1
Calcule a tangente do ângulo para descobrir a distância horizontal entre objetos. Tome como exemplo um ângulo que mede 60 graus. A tangente de 60 graus é √3 ou 1,732.
Step 2
Divida a altura do objeto pela tangente do ângulo. Continuando com o exemplo, digamos que a altura do objeto em questão é 150 metros. 150 dividido por 1,732 é 86,603. A distância horizontal entre o ponto em questão e o objeto é 86,603 metros.
Step 3
Calcule o seno do ângulo para encontrar a distância total entre os objetos, ou a hipotenusa. Por exemplo, o seno de 60 graus é √3/2 ou 0,866.
Step 4
Divida a altura do objeto pelo seno do ângulo. Por exemplo, 150 dividido por 0,866 resulta em 173,205. A distância total entre os objetos é 173,205 metros.
Referências
Sobre o Autor
Chance E. Gartneer began writing professionally in 2008 working in conjunction with FEMA. He has the unofficial record for the most undergraduate hours at the University of Texas at Austin. When not working on his children's book masterpiece, he writes educational pieces focusing on early mathematics and ESL topics.
Créditos Fotográficos
Comstock/Stockbyte/Getty Images