Como calcular o volume de um trapezóide?
math image by jaddingt from Fotolia.com
Entender o processo matemático envolvido no cálculo do volume de um trapezoide passa pelo coração da geometria da construção científica conceitual e prática. O texto abaixo é um procedimento passo a passo, para primeiro compreender os princípios fundamentais que acompanham as variáveis da equação formulada essencial, e depois utilizá-la para resolver problemas com figuras trapezoidais.
Step 1
Entender que a construção de projetos práticos, tais como prédios residenciais ou comerciais, trabalhos em solo como camas de lodo e tubulações domiciliares e outras instalações, envolvem o conhecimento necessário do volume de substâncias líquidas dentro de figuras planas fechadas, que irá permitir ao estudante o entendimento da necessidade de se calcular o volume. A medição precisa de dimensões existentes leva a um cálculo preciso do volume.
De forma prática, encontrar trapezoides como cortes transversais de paredes de argila na bacia geográfica são úteis ao se definir um trapezoide. Se dois lados de uma figura de quatro lados são paralelos, mas não iguais em tamanho, e os outros dois lados não são paralelos, essa figura é chamada de trapezoide.
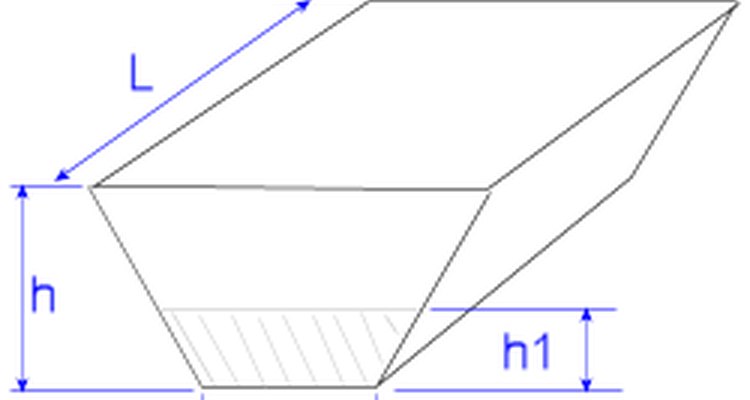
Então, se você tem uma figura que tenha 22,86 m de comprimento, com a dimensão frontal de 17,37 m de largura e 10,66 m de altura, e que tenha um fundo de 21.94 m de largura e 3,65 m de altura, calcular o volume seria proceder da seguinte maneira:
-
A forma pode ser pensada como um retângulo de 17,37 x 22,86 na frente, unida a planos de 21,94 x 3,65 no fundo, a uma distância de 22,86 m.;
-
A fórmula de cálculo do volume dessa forma, que pode ser desenhada como um tronco com um topo e fundo retangulares ao invés da frente e costas, pode ser expressada como V=[a1b1 + a2b2 + (a1b2 + a2b1)/2] * h/3, onde as variáveis podem ser descritas por a1= 17,37; b1=10,66; a2=21,94; b2=3,65; h=22,86: V=[a1b1 + a2b2 + (a1b2 + a2b1)/2] * h/3 V=[17,3710,66 + 21,943,65 + (17,373,65 + 21,9410,66)/2] * 22,86/3 V=[265,60 + (63,54 + 234,11)/2] * 7,62 V=[265,60 + (297,66)/2] 7,62 V=[414,44] 7,62 V=3.158,03 m³
Step 2
Seguindo o formato, o volume dinâmico de um trapezoide difere daquele do modelo estático devido a que um trapezoide estático é geometricamente uma figura com duas dimensões. A área a ser computada pode somente ser de um trapezoide desenhado em duas dimensões em papel. Por isso, uma versão alternativa da fórmula, usando a média de largura e comprimento é: V=[a1b1 + a2b2 + 4((a1+a2)/2 * (b1+b2)/2)] * h/6 O retângulo tem lados que são a média dos lados dos retângulos do topo e fundo.
Step 3
Agindo como na aplicação dinâmica do passo 2, o volume de uma construção trapezoidal, como uma piscina ou um cilindro fechado, pode ser computada como litros por metro de uma altura específica. Isso significa que o volume de um contêiner cheio dividido pela sua altura rende a razão própria — use a fórmula (com dimensões em m) para obter metros cúbicos.
Para qualquer contêiner que não seja cilíndrico, a razão irá variar com a profundidade, caso o aluno deseje. E alguém poderá pensar que isso significa que o contêiner estaria parcialmente cheio e que o volume seria determinado a níveis diferentes. Isto é, o volume é uma função da altura.
Step 4
Indo um pouco mais adiante, como a largura na direção 'a' muda linearmente de a1 para a2, a = a1 + (a2-a1)k = (1-k)a1 + ka2; ao que unidades kh sobem do fundo (onde k varia de 0 a 1); da mesma forma, b = b1 + (b2-b1)k = (1-k)b1 + kb2; o volume do sólido com a altura kh, base a1 por b1 e topo a por b é V(k) = [a1b1 + ab + a1b/2 + ab1/2] * kh/3.
Se utilizarmos o nível real de líquido ao invés da razão k, podemos substituir k = L/h e obteremos V(L) = [(3h^2-3Lh+L^2)a1b1 + L^2a2b2 + (3Lh-2L^2)(a1b2 + a2b1)/2] * L/(3h^2). Isso nos dá o volume como função da profundidade.
Step 5
Computar o volume de um trapezoide adequadamente envolve a habilidade de interpretar se a figura trapezoidal é bidimensional ou tridimensional. A prática dinâmica do aspecto da engenharia de interpretação trapezoidal gira em torno de saber se a figura trapezoidal é algo que é simplesmente desenhado ou construído, quer contenha um volume ou seja mero esboço em um papel.
Mais Artigos
Dica
- Resolver um problema geométrico permite ao estudante entender como e porque a fórmula é da forma que é, e porque a altura é uma variável tão importante. Checar a resposta obtida manualmente com, por exemplo, uma calculadora científica Hewlett-Packard é uma boa maneira de conseguir total precisão.
Créditos Fotográficos
math image by jaddingt from Fotolia.com






