Step 1

Determine o comprimento de um lado do hexágono. Para hexágonos regulares, todos os lados são iguais: dessa forma todos os lados tem o mesmo comprimento e se um dos lados é conhecido, então todos são. O lado conhecido é chamado de "g" (lado dado).

Step 2

Escreva a equação para encontrar a diagonal de um hexágono regular: d(diagonal) = 2g (lado dado).

Step 3

Multiplique o lado conhecido do hexágono por 2. O produto é o comprimento da diagonal de um hexágono regular.

Step 4

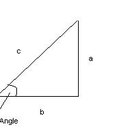
Embora você possa calcular o número de diagonais de um hexágono irregular, encontrar o comprimento da diagonal de um irregular exigiria, primeiramente, a divisão do hexágono em quatro triângulos. No entanto, se não existirem triângulos equiláteros no hexágono irregular, o que é o mais capaz de acontecer, não há uma formal para encontrar o comprimento do lado interior, o que seria a diagonal. O Teorema de Pitágoras se aplica apenas aos triângulos retângulos, se cada lado e ângulo forem dados juntos com a área, então as diagonais poderiam ser determinadas, mas haveria um monte de variáveis.