Como calcular a trajetória de uma bala
Credit: NASA
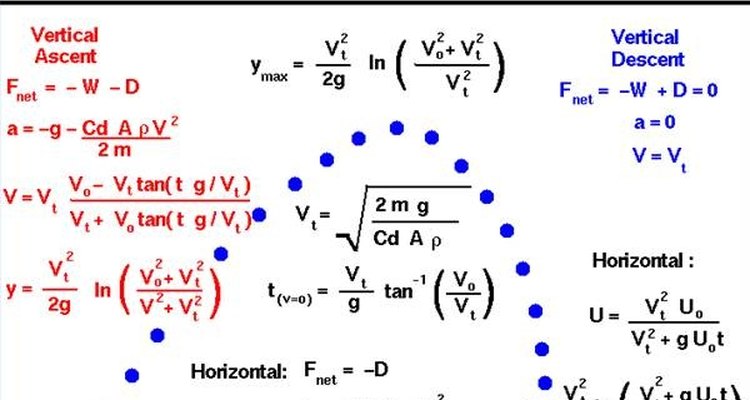
Eis aqui o método para calcular a trajetória de uma bala e, especificamente, o tempo no ar, o alcance e o mais alto ponto de sua trajetória. Neste exemplo, algumas suposições foram feitas para simplificar o cálculo: resistência do ar desprezível, sem vento e distância de disparo insuficiente para a rotação da Terra ter efeito.
Determinar o tempo no ar.
Step 1
Em primeiro lugar, o formato do arco deve ser determinado. Se o ângulo for inicialmente para baixo, então o ponto mais alto já é conhecido por ser a posição de tiro. Ate mesmo um ângulo para cima pode ter o alvo como o ponto mais alto, se este ângulo é raso ou com altura (h) suficiente. Isto pode ser determinado no passo quatro, quando é determinado o tempo no ar.
Step 2
Se o ângulo "?" de disparo é aquele entre a trajetória inicial do projétil e a horizontal, então a velocidade inicial vertical é V(i)= V.sen?.
Step 3
O tempo no ar é encontrado usando-se a equação da posição h= V.sen?.t - (0,5)g.t^2, onde g= 9,8 metros/segundos^2. Todas as variáveis são conhecidas, exceto o tempo no ar, t, então esta pode-se resolver utilizando a função quadrática: ax^2 + bx + c = 0, logo, x = [ -b ± √(b^2-4ac) ] / 2a
Step 4
Se mais de uma solução para t é permitida, pois h>0, então o primeiro resultado corresponde à quando altura=h na trajetória da subida, e o segundo a quando a altura=h no caminho de descida. Se h<0, então a única solução real para t foi permitida, e a outra é negativa.
Determine a altura máxima
Step 1
Se ?<0, logo, já se sabe que a altura máxima é a altura inicial, h=0.
Step 2
Se houvesse mais de uma vez, t, em que a bala altinge h, então o menor t corresponde a um caminho de voo onde h é o ponto mais alto. O maior t corresponde a bala atingindo uma maior altura antes de retornar para h, para solucionar esta altura, usa-se a formula V(t)= V(0)- 9,8t para encontrar o valor de t quando a velocidade vertical for zero. Em outras palavras, para que tempo, t, V.sen?= 9.8t.?
Step 3
Resolvendo t e ligando a fórmula de altura, têm-se a altura máxima: hm= V.sen? - 4,9t^2. A mesma abordagem é usada para solução da altura máxima, se somente uma solução para t foi permitida.
Determine a distância horizontal percorrida.
Step 1
Para determinar a distância horizontal percorrida pelo tempo o qual a bala atinge a altura h, primeiro calcule a velocidade horizontal inicial da bala: v(i)= V.cos(?).
Step 2
Substituia o tempo, t, quando a bala chegar à altura final, A, na posição da fómula que utiliza a velocidade horizontal: A= V.cosΘ.t. Assumindo que não há resistencia do ar e nenhum termo de aceleração no lado direito.
Step 3
Se houve mais de um tempo t quando a altura estava em h, então as duas posições de "A" serão válidas, com o ponto mais alto alcançado sendo hm para o menor dos dois "A". As posições finais horizontais e verticais e o ponto mais alto alcançado agora são conhecidos, assim determinando a trajetória da bala.
Referências
Recursos
Sobre o Autor
Paul Dohrman's academic background is in physics and economics. He has professional experience as an educator, mortgage consultant, and casualty actuary. His interests include development economics, technology-based charities, and angel investing.
Créditos Fotográficos
Credit: NASA